s01: NumPy#





This is a quick introduction to the Numpy package.

Objectives of this session:#

  • Understand the Numpy array object

  • Be able to use basic NumPy functionality

  • Understand enough of NumPy to seach for answers to the rest of your questions ;)

So, we already know about python lists, and that we can put all kinds of things in there. But in scientific usage, lists are often not enough. They are slow and not very flexible.

# first things first, import the package
import numpy as np

What is an array?#

For example, consider [1, 2.5, 'asdf', False, [1.5, True]] - this is a Python list but it has different types for every element. When you do math on this, every element has to be handled separately.

NumPy is the most used library for scientific computing. Even if you are not using it directly, chances are high that some library uses it in the background. NumPy provides the high-performance multidimensional array object and tools to use it.

An array is a ‘grid’ of values, with all the same types. It is indexed by tuples of non negative indices and provides the framework for multiple dimensions. An array has:

  • data - raw data storage in memory.

  • dtype - data type. Arrays always contain one type

  • shape - shape of the data, for example 3×2 or 3×2×500 or even 500 (one dimensional) or [] (zero dimensional).

a = np.arange(1,17,1)

\[\begin{bmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 \end{bmatrix}\]

a = np.arange(1,17,1).reshape(4, 4)

\[\begin{split}\begin{bmatrix} 1 & 2 & 3 & 4\\ 5 & 6 & 7 & 8\\ 9 & 10 & 11 & 12\\ 13 & 14 & 15 & 16 \end{bmatrix}\end{split}\]

Creating arrays#

There are different ways of creating arrays (numpy.array(), numpy.ndarray.shape, numpy.ndarray.size):

a = np.array([1,2,3])               # 1-dimensional array 
b = np.array([[1,2,3],[4,5,6]])     # 2-dimensional array 

b.shape                             # the shape (rows,columns)
b.size                              # number of elements

6

In addition to above ways of creating arrays, there are many other ways of creating arrays depending on content (numpy.zeros(), numpy.ones(), numpy.arange(), numpy.linspace()):

np.zeros((2, 3))             # 2x3 array with all elements 0
np.ones((1,2))               # 1x2 array with all elements 1

np.arange(10)                # Evenly spaced values in an interval
np.linspace(0,9,10)          # same as above, see exercise

c = np.ones((3,3))
d = np.ones((3, 2), 'bool')  # 3x2 boolean array

In many occasions (especially when something goes different than expected) it is useful to check and control the datatype of the array (numpy.ndarray.dtype, numpy.ndarray.astype()):

d.dtype                    # datatype of the array
d.astype('int')            # change datatype from boolean to integer

array([[1, 1],
       [1, 1],
       [1, 1]])

Array maths and vectorization#

Clearly, you can do math on arrays. Math in NumPy is very fast because it is implemented in C or Fortran - just like most other high-level languages such as R, Matlab, etc do.

By default, basic arithmetic (+, -, *, /) in NumPy is element-by-element. That is, the operation is performed for each element in the array without you having to write a loop. We say an operation is “vectorized” when the looping over elements is carried out by NumPy internally, which uses specialized CPU instructions for this that greatly outperform a regular Python loop.

a = np.array([[1,2],[3,4]])
b = np.array([[5,6],[7,8]])

# Addition
c = a + b
d = np.add(a,b)

# Standard stats
d_mean = np.mean(d)
print("The mean of d is {}".format(d_mean))

The mean of d is 9.0

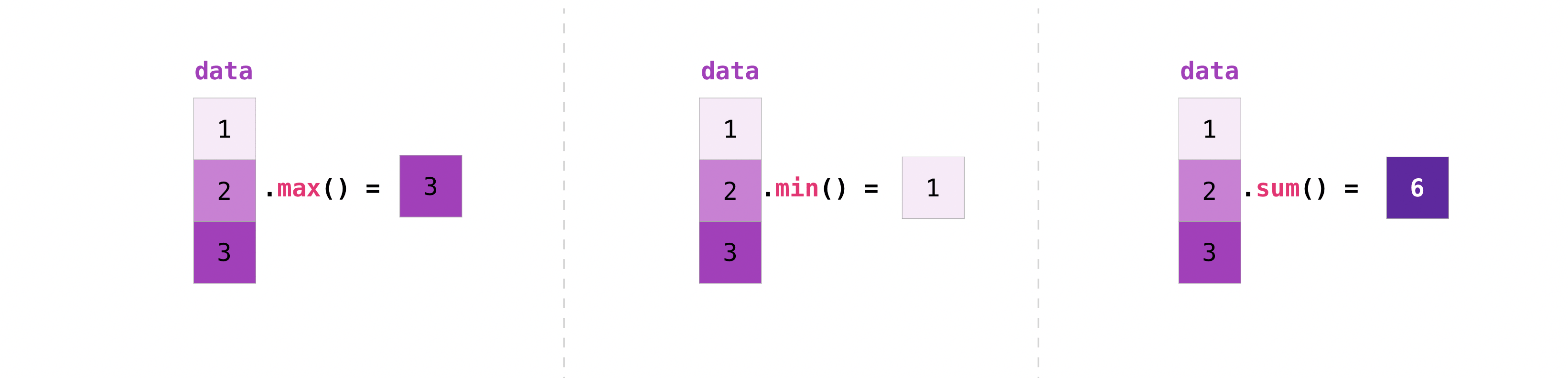
Imagine you have the numpy array as a variable (data in the example below). On this array you can perform numpy functions such as max, min or sum, just to name a few.



Indexing and Slicing#

See also Numpy basic indexing docs

Using positional indexing, you can select a subset of the array by adressing row and/or columns using brackets ([]). See the example below.



In positional indexing you can specify up to three inputs. The basic syntax is [i:j:k] where i is the starting index, j is the stopping index, and k is the step. See the examples provided by numpy.

NumPy has many ways to extract values out of arrays:

  • You can select a single element

  • You can select rows or columns

  • You can select ranges where a condition is true.

a = np.arange(1,17,1).reshape(4, 4)  # 4x4 matrix from 0 to 15
a[0]                             # first row
a[:,0]                           # first column
b = a[1:3,1:3]                   # middle 2x2 array

idx = (a > 5)      # creates boolean matrix of same size as a
a[idx]             # array with matching values of above criterion

a[a > 5]           # same as above in one line

print(idx)

[[False False False False]
 [False  True  True  True]
 [ True  True  True  True]
 [ True  True  True  True]]
Task 1.5: Create a random array with elements between 0 and 1. Then add 10 to all elements in the range [0.2, 0.7). (2 points)

Types of operations#

There are different types of standard operations in NumPy:

  • One, two, or three input arguments

  • For example, a + b is similar to np.add(a, b) but the ufunc has more control.

  • out = output argument, store output in this array (rather than make a new array) - saves copying data!

  • A very comprehensiv and easy overview can be found here

If you have a multiple dimensional array, you can specify the axis over which the operations should be done using the key axis = in the numpy functions. 



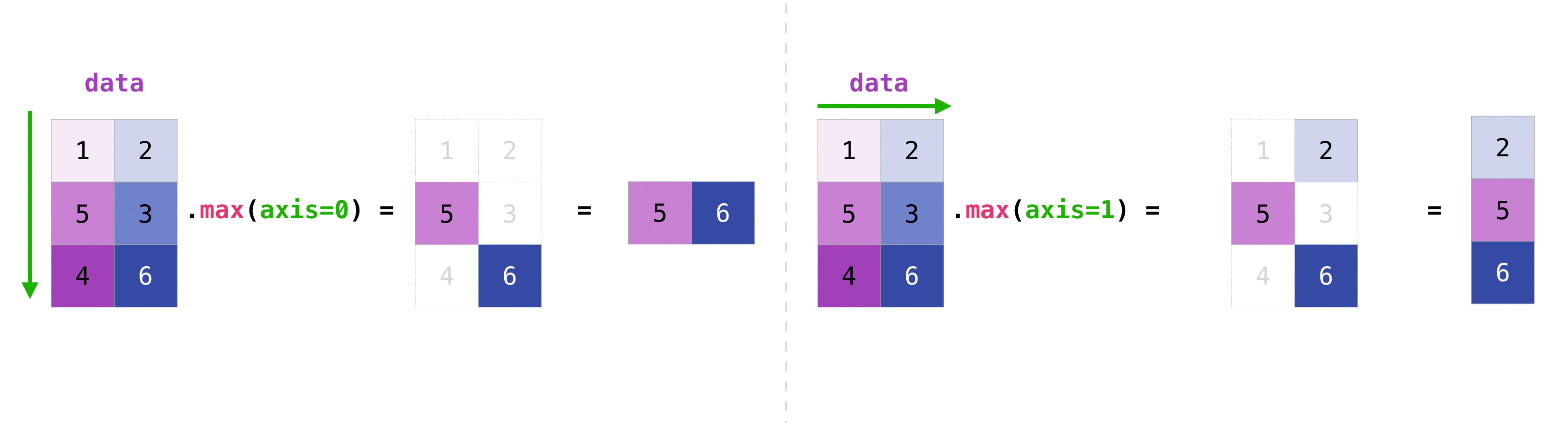
x = np.arange(12).reshape(3,4)
                    #  array([[ 0,  1,  2,  3],
                    #         [ 4,  5,  6,  7],
                    #         [ 8,  9, 10, 11]])

x.max()             #  11
x.max(axis=0)       #  array([ 8,  9, 10, 11])
x.max(axis=1)       #  array([ 3,  7, 11])

x

array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])
Task 1.6:
    Create a (8, 8)-array called chess with a chessboard pattern (use the values 0 and 1 for this). There are many possible solutions, feel free to give several variants. For example, see the help for the function np.tile, or first create an array of all zeros and then insert ones at the appropriate places (e.g. by indexing appropriately). (3 points)